Robot sigue líneas con Arduino
Este artículo trata sobre la construcción y programación de un robot que sigue líneas con Arduino y un sensor de infrarojos.
Construcción del Robot
Materiales
El chasis que verás en las fotos es específico, creado a medida por la empresa What's Next? para el proyecto [Robots Boost Skills]. El resto de componentes son genéricos y se pueden comprar Arduinos oficiales, What's Next Yellow o cualquier clon compatible.
Esta es la lista de materiales:
- Chasis que permita 2 ruedas con motor DC analógicos y una rueda delantera.
- 2 Motores DC analógicos con reducción y ruedas.
- Arduino Uno o equivalente.
- 1 Sensor Pololu QTR-8A o QTR-8RC
- Arduino Motor Shield o alguno que tenga el mismo Chip L298
- Baterías, entre 9V y 12V
Construcción del Chasis
En el caso del robot del ejemplo, el chasis tiene todos los elementos necesarios. Si lo tienes que construir, aquí tienes algunos consejos:
- Se recomienda cuidar el centro de gravedad de robot para que no plante rueda y tenga la adherencia necesaria. Por ejemplo, las baterías deberían estar entre las ruedas motrices y la rueda delantera.
- La distancia al suelo del sensor infrarojo es muy importante, ha de estar muy cerca, pero no rozar.
- Hay que dejar espacio para los cables y para poder modificar las conexiones sin necesidad de desmontar todo el robot.
El sensor
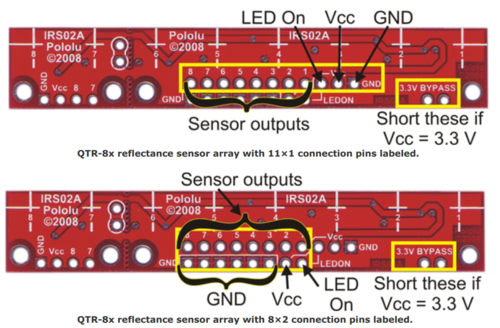
En nuestro caso, el sensor QTR-8[A-RC] es un conjunto de 8 emisores y sensores infrarrojos en un mismo circuito. Esto permite una gran precisión, ya que tienes 8 lecturas cada vez. Los sensores están separados entre ellos 9,52mm. Estos sensores tienen una distancia al suelo recomendada de 3mm y un máximo de 6mm para el QTR-A y 9.5mm para el QTR-8RC.
La salida de los dos sensores es diferente, (analógica o digital), por lo que es importante distinguirlos y decidir cual vamos a usar. En nuestro caso, tenemos el QRT-8RC, por lo que, a partir de aquí, todo el manual se basa en este.
Puesto que vamos a usar 5V para alimentarlo, no es necesario unir los pines de 3.3V Bypass
Podemos conectar el pin LEDON que permite indicar con HIGH, LOW o PWM el estado de los LEDs. Si los apagamos, podemos consumir menos energía cuando no está leyendo.
El QTR8-RC mide la reflectancia con el tiempo entre un estado HIGH y uno LOW del pin de I/O.
La lectura típica en el QTR8-RC es la siguiente:
- Encender los LEDs (opcional)
- Poner la linea I/O a una salida y ponerla en HIGH.
- Dejar al menos 10 μs al sensor para que arranque.
- Poner la I/O a Input
- Medir el tiempo que tarda el voltaje en caer esperando a la I/O a que vuelva a LOW.
- Apagar los LEDs (opcional)
Estos pasos se pueden hacer en varias líneas I/O al mismo tiempo. Con mucha reflectividad, el tiempo de bajada a LOW debe ser mínimo. Con poca (superficie negra) el tiempo debe mayor. Esto funciona porque para leer hay un fototransistor y un capacitor, este recibe un HIGH y en función de la intensidad de la luz, tarda más o menos en quedarse en estado de LOW. De esta manera, con el color blanco tardará unos pocos microsegundos y con el negro unos pocos milisegundos. Puesto que en aproximadamente 1ms se tienen lecturas y se puede leer de todos los sensores a la vez esto da aproximádamente la capacidad de leer hasta a 1kHz, es decir, 1000 lecturas por segundo.
Si se necesitan lecturas a mucha frecuencia, se recomienda que el sensor esté muy cerca del suelo, recomendado 3,5 mm i máximo 9 mm.
Cuanto más lejos peor lecturas y cuanta más luz ambiental peor. Si es necesario, bloquearemos la luz ambiental con cinta aislante o similar.
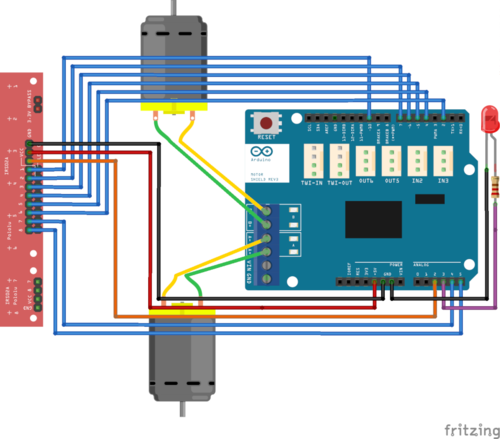
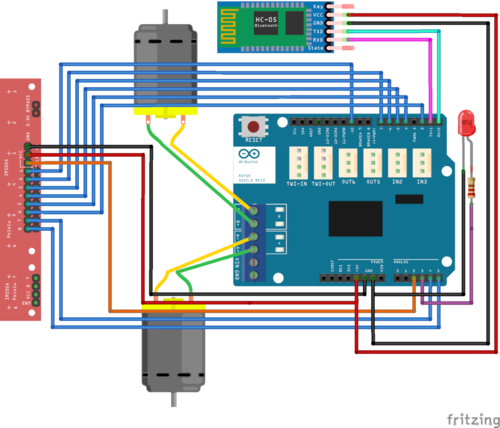
De esta manera, el esquema de conexiones del robot queda de la siguiente manera:
Programación del robot
Nuestro robot, al igual que el Robot esquiva obstáculos con Arduino va leyendo los sensores y, en función de esto, va modificando la velocidad de las ruedas. A diferencia de los sensores de ultrasonidos, estos sensores veremos que no nos dan los datos en crudo. Por otro lado, son muy ràpidos haciendo las lecturas y no necesitan que pase un tiempo entre lecturas. Este sensor viene con una completa biblioteca con funciones que dan los datos ya tratados. No necesitamos hacer medias ni descartar valores extremos. La biblioteca calibra los sensores según las condiciones del circuito y nos da lo que calcula a partir de los datos que obtiene.
Leyendo del sensor
Para que funcione, necesitamos la biblioteca correspondiente. En los últimos Arduino IDE es tan simple como ir al gestor de Bibliotecas y importar la QTRSensors.
La biblioteca funciona tanto para el QTR-8RC como el QTR-8A, pero cambia la manera de configurarlo:
// Crear un objeto para 8 sensores en los pines digitales 2,4,5,6,7,10 y en los analogicos A4 A5
QTRSensors qtr;
qtr.setTypeRC();
qtr.setSensorPins((const uint8_t[]){19,18,2,4,5,6,7,10}, 8);
qtr.setEmitterPin(16);
Calibrar los sensores es lo primero que debería hacer el robot. Así, en la rutina de inicialización (setup), se recomienda lanzar este código:
void setup()
{
pinMode(A3, OUTPUT); // LED para indicar que está calibrando
// Configuración de los sensores. Aquí ya usamos los que quedan libres del motor shield.
qtr.setTypeRC();
qtr.setSensorPins((const uint8_t[]){19,18,2,4,5,6,7,10}, SensorCount);
qtr.setEmitterPin(16);
delay(500);
digitalWrite(A3, HIGH); // Encendemos un led conectado a A3 para indicar que estamos calibrando
// 2.5 ms RC read timeout (default) * 10 reads per calibrate() call
// = ~25 ms per calibrate() call.
// Call calibrate() 400 times to make calibration take about 10 seconds.
for (uint16_t i = 0; i < 400; i++)
{
qtr.calibrate();
}
digitalWrite(A3, LOW); // Ya ha calibrado
// Imprimir los valores mínimos obtenidos cuando se calibraba:
Serial.begin(9600);
for (uint8_t i = 0; i < SensorCount; i++)
{
Serial.print(qtr.calibrationOn.minimum[i]);
Serial.print(' ');
}
Serial.println();
// Imprimir los valores máximos obtenidos al calibrar:
for (uint8_t i = 0; i < SensorCount; i++)
{
Serial.print(qtr.calibrationOn.maximum[i]);
Serial.print(' ');
}
Serial.println();
Serial.println();
delay(1000);
}
Para leer del sensor, se puede usar la función readCalibrated() o read(). Con readCalibrated(), los valores obtenidos serán entre 0 (blanco) y 1000 (negro). Esto lee un sensor en concreto y retorna su lectura. Estos datos son en 'crudo' y pueden servir para todo tipo de automatismos o robots, pero para seguir líneas, la biblioteca de Pololu tiene sus funciones específicas.
Para la detección de líneas, se usar la función readLineBlack() si la línea es negra. El resultado de esta función es 0 si la línea está dentro o fuera de sensor 0 y 1000*(N-1) para cada sensor. Los valores para 8 sensores pueden ser, por tanto, 0, 1000, 2000 ... 7000 dependiendo de la posición de la línea.
Hemos modificado el código de ejemplo de la biblioteca para analizar los valores que obtiene el sensor con nuestros 8 sensores:
#include <QTRSensors.h>
// This example is designed for use with eight RC QTR sensors. These
// reflectance sensors should be connected to digital pins 3 to 10. The
// sensors' emitter control pin (CTRL or LEDON) can optionally be connected to
// digital pin 2, or you can leave it disconnected and remove the call to
// setEmitterPin().
//
// The setup phase of this example calibrates the sensors for ten seconds and
// turns on the Arduino's LED (usually on pin 13) while calibration is going
// on. During this phase, you should expose each reflectance sensor to the
// lightest and darkest readings they will encounter. For example, if you are
// making a line follower, you should slide the sensors across the line during
// the calibration phase so that each sensor can get a reading of how dark the
// line is and how light the ground is. Improper calibration will result in
// poor readings.
//
// The main loop of the example reads the calibrated sensor values and uses
// them to estimate the position of a line. You can test this by taping a piece
// of 3/4" black electrical tape to a piece of white paper and sliding the
// sensor across it. It prints the sensor values to the serial monitor as
// numbers from 0 (maximum reflectance) to 1000 (minimum reflectance) followed
// by the estimated location of the line as a number from 0 to 5000. 1000 means
// the line is directly under sensor 1, 2000 means directly under sensor 2,
// etc. 0 means the line is directly under sensor 0 or was last seen by sensor
// 0 before being lost. 5000 means the line is directly under sensor 5 or was
// last seen by sensor 5 before being lost.
QTRSensors qtr;
const uint8_t SensorCount = 8;
uint16_t sensorValues[SensorCount];
void setup()
{
pinMode(A3, OUTPUT); // LED para indicar que está calibrando
// Configuración de los sensores. Aquí ya usamos los que quedan libres del motor shield.
qtr.setTypeRC();
qtr.setSensorPins((const uint8_t[]){19,18,2,4,5,6,7,10}, SensorCount);
qtr.setEmitterPin(16);
delay(500);
digitalWrite(A3, HIGH); // Encendemos un led conectado a A3 para indicar que estamos calibrando
// 2.5 ms RC read timeout (default) * 10 reads per calibrate() call
// = ~25 ms per calibrate() call.
// Call calibrate() 400 times to make calibration take about 10 seconds.
for (uint16_t i = 0; i < 400; i++)
{
qtr.calibrate();
}
digitalWrite(A3, LOW); // Ya ha calibrado
// Imprimir los valores mínimos obtenidos cuando se calibraba:
Serial.begin(9600);
for (uint8_t i = 0; i < SensorCount; i++)
{
Serial.print(qtr.calibrationOn.minimum[i]);
Serial.print(' ');
}
Serial.println();
// Imprimir los valores máximos obtenidos al calibrar:
for (uint8_t i = 0; i < SensorCount; i++)
{
Serial.print(qtr.calibrationOn.maximum[i]);
Serial.print(' ');
}
Serial.println();
Serial.println();
delay(1000);
}
void loop()
{
// Lee los sensores calibrados para obtener una posición de la línea de 0 a 7000
// En este caso, la línea es negra, para blanca usamos readLineWhite()
uint16_t position = qtr.readLineBlack(sensorValues);
// Pintar los valores de los sensores de 0 a 1000 donde 1000 significa negro y 0 blanco
for (uint8_t i = 0; i < SensorCount; i++)
{
Serial.print(sensorValues[i]);
Serial.print('\t');
}
// Al final de la línea la posición:
Serial.println(position);
delay(250);
}
El resultado puede dar algo como esto:
292 292 244 196 244 292 244 292 <-- Los valores mínimos de cada sensor 772 2500 2500 2500 2500 2500 2500 2500 <-- Los valores máximos de cada sensor 16 3 1 1 1 1000 521 3 5342 <-- Donde pone 1000 está la línea 0 0 0 0 0 23 1000 219 6179 <-- El 6179 indica que está en el sensor 7 0 0 0 0 0 23 1000 411 6291 8 1 0 0 0 170 1000 50 5854 0 0 0 0 19 1000 235 0 5190 8 1 0 20 1000 992 23 1 4497 108 0 19 1000 544 0 19 0 3133 <-- Observa el el sensor 4 tiene 1000 y la posición indica 3133 (N-1 sensor) 0 21 1000 342 0 0 0 0 2254 8 1 590 1000 23 1 0 1 2628 100 0 0 503 1000 21 19 0 3436 108 0 0 19 1000 1000 19 0 4269 0 0 0 19 0 1000 1000 0 5500 16 3 0 0 0 3 1000 1000 6500 0 0 0 0 0 0 1000 871 6465 0 0 0 0 0 1000 659 0 5397 0 0 0 204 1000 50 21 0 3830 0 0 634 1000 19 0 19 0 2611 8 534 1000 22 1 1 1 1 1651 0 894 1000 19 0 0 0 0 1527 0 483 1000 19 0 0 0 0 1674 8 1 1000 1000 0 1 0 1 2500 100 0 234 1000 42 0 17 0 2599
Ejemplo del manual oficial del sensor para un sigue líneas simple con 3 sensores:
En este ejemplo, usamos los 8 sensores disponibles:
PID
El anterior ejemplo ya funciona razonablemente bien en una línea. No obstante, si queremos aplicar más velocidad, el tiempo de reacción y el error acumulado hace que se pueda salir de la línea. Por ello necesitamos una manera de corregir el rumbo antes de que sea demasiado tarde y suavizar el comportamiento del robot.
La lectura de qtr.readLineBlack(sensorValues); Retorna un número. En caso de utilizar los 8 sensores, el número va de 0 a 7000, siendo cada 1000*(N-1) para sensor. De esta manera, si está en el 3456, por ejemplo, quiere decir que está en el sensor 4, aunque parte de la línea está en el sensor 5. Así, lo ideal es que esté más o menos en esa posición, ya que el 4 y 5 son los sensores centrales. Por eso, en el ejemplo anterior calculamos el error como position - 3500. O en el ejemplo de 3 sensores era -1000.
Nuestra estrategia, al contrario que en los ejemplos anteriores, es fijar una velocidad base y calcular una corrección a esa velocidad en función del cálculo que se haga con el error obtenido de los sensores:
velocidad_izquierda = base_izquierda + corrección velocidad_derecha = base_derecha - corrección
Para conseguir un buen valor para la corrección de la velocidad, podemos usar una estratégia usada en muchos ámbitos de la automatización, el PID (Proporcional, Integral, Derivativo). Este intentará corregir el rumbo tan rápido como el robot pierda la línea. Hay numerosos estudios y artículos matemáticos y electrónicos que hablan de este tema con complejas ecuaciones. Sin embargo, el funcionamiento fundamental se puede entender de forma intuitiva y no es necesario, en nuestro caso, recurrir a la teoría matemática de porqué funciona.
El PID es un proceso de realimentación, en el que un sistema tiene como entradas las lecturas de los sensores, hace unos cálculos y acciones que afectan físicamente al sistema y, por tanto a las mediciones posteriores. La diferencia entre el valor medido y el valor que se espera obtener (objetivo) es el error. El PID tiene éxito cuando consigue que el error sea mínimo en todas las lecturas. Otro factor de éxito es cuando lo consigue en poco tiempo y, en nuestro caso, el robot acaba antes el circuito. A este éxito se le llama Sistema en equilibrio.
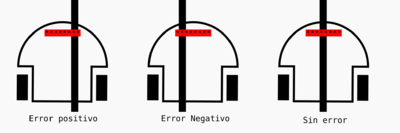
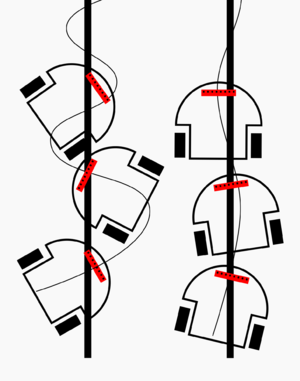
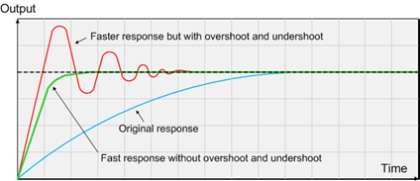
En el siguiente dibujo se representa (exagerando un poco) una situación mala en la que el robot sigue la línea pero da bandazos a los dos lados y incluso se sale en ocasiones de la misma y otro en el que sigue la línea mucho más ajustado.
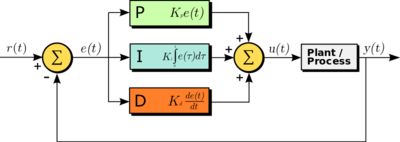
Dentro de la nomenclatura, el Set Point nuestro es la línea. Si la línea no está centrada, hay un error, este error es el que recibe el algoritmo y el algoritmo produce una salida. Esta salida, en nuestro caso, la velocidad de cada rueda, produce un cambio en el robot que provoca nuevas lecturas diferentes que serán comparadas con el Set Point de nuevo para ver si ha aumentado el error o disminuido. La lectura de los sensores y la toma de decisiones tarda un tiempo T, la inversa de T es la frecuencia de muestreo o f y cuanto mayor sea, mejor. La salida del algoritmo PID es la suma de 3 cálculos P + I + D que vamos a detallar a continuación:
Control Proporcional
A continuación, vamos a utilizar la palabra "control", ya que estos conceptos son ampliamente utilizados en la robótica y el control industrial. Todo automatismo que intenta mantener un control (temperatura, nivel de agua, posición...) en función de lecturas de sensores, ha de tener una estrategia para hacerlo de la forma más inteligente posible. En el ejemplo básico inicial, el robot va dando bandazos de un lado a otro corrigiendo el rumbo sin parar. La idea es que corrija el rumbo antes de tener que hacerlo de forma tan brusca.
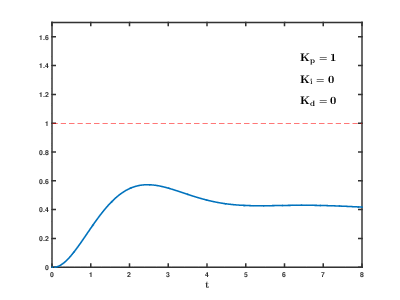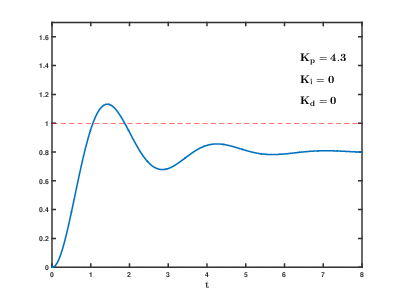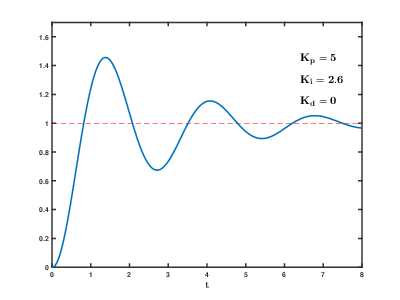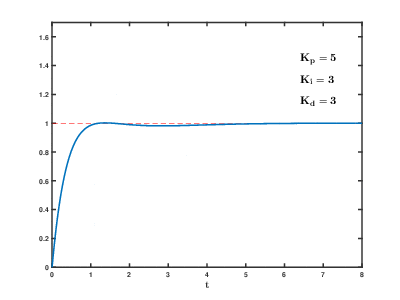
En el control proporcional, corregimos más o menos en función de la cantidad de error en este instante, por eso podemos decir que es una reacción en el presente. Para ello, podemos establecer un coeficiente proporcional (Kp)
error = posición - 3500 corrección = Kp * error velocidad_izquierda = base_izquierda + corrección velocidad_derecha = base_derecha - corrección
Como se puede observar, a mayor error, mayor corrección. También se puede observar que no hemos dado un valor determinado a Kp. Este valor se consigue por prueba y error, de la misma manera que la velocidad base de las ruedas. A mayor velocidad base, más rápido va el robot y más posible es que se salga. A mayor Kp, mayor corrección y, por tanto, una respuesta más rápida, pero a cambio de giros más bruscos. Si se produce Overshoot, vuelve bruscamente al sitio, provocando un Overshoot en el otro lado. Esto puede estabilizarse o, por el contrario, bailar cada vez más hasta que se salga.
Control Integral
El control Proporcional ya es una mejora, pero en realidad sólo tiene en cuenta el error instantáneo y no sabe si se está acumulando error o es algo puntual. El control Integral va sumando los errores del pasado y permite averiguar si la dirección del robot está empeorando su posición. Es más, si el robot pierde la línea, la integral "recordará" por donde veía el error y podrá retornar el robot a la línea.
En el algoritmo anterior, añadimos la variable integral, (que inicialmente vale 0) y un nuevo coeficiente Ki
error = posición - 3500 integral = integral + error corrección = Kp * error + Ki * integral velocidad_izquierda = base_izquierda + corrección velocidad_derecha = base_derecha - corrección
Al igual que el otro coeficiente, el Ki también hay que ajustarlo por prueba/error.
La Integral tiene una serie de ventajas añadidas al control proporcional:
- El control proporcional es el más efectivo, pero puede provocar un error residual que no puede vencer por rozamientos, velocidades poco precisas de los motores o demás. Este error es tan pequeño que el control proporcional, al ser proporcional al error, no puede solucionar. La integral va sumando esos pequeños errores y los magnifica hasta que los soluciona.
- Si el robot pierde completamente la línea, la suma de errores previa será muy grande, pero la parte proporcional del algoritmo no detecta nada. La integral es lo único que queda que "recuerda" por dónde viene el error y acaba retornando el robot a su línea. Si se ha salido, es un Overshoot muy importante y la acumulación tanto tiempo de error es muy grande y puede que la integral provoque un Overshoot cuando el lado contrario no compense la suma. Esto lo solucionamos más adelante.
Control Derivativo
Esta tercera estrategia sirve para detectar si el error está aumentando. Lo que hace es comparar el error actual con el pasado. Esto permite solucionar cambios bruscos de dirección. En cierta manera, predice qué va a pasar y actúa con los datos del futuro. El concepto de derivada viene de calcular cómo de rápido está cambiando el error.
error = posición - 3500 integral = integral + error derivativa = error - error_anterior corrección = Kp * error + Ki * integral + Kd * derivativa velocidad_izquierda = base_izquierda + corrección velocidad_derecha = base_derecha - corrección
error_anterior = error
El Kd también se ajusta por prueba y error.
La derivativa se calcula como derivativa = error - error_anterior. Tal vez sea la más difícil de entender de forma intuitiva. Pensemos en los casos que se pueden dar (suponemos un Kd=1, Kp=1 y Ki=0 para simplificar los cálculos):
- El robot tiene un error de -24 y luego de -31: derivativa = -31 - -24 = -7 ; El error está aumentado en -7, es decir hacia el lado negativo. Por tanto, la corrección será Kp*-31 + -7 = -38. La derivativa ha aumentado la corrección contra el lado negativo un poco, ya que percibe que aún el robot está desviandose hacia ese lado.
- El robot tiene un error de -24 y luego de -10: derivativa = -10 - -24 = 14; El error está disminuyendo en 14 hacia el lado positivo: corrección = -10 + 14 = 4. Aunque el robot está, de momento, en el lado negativo, ha disminuido mucho ese error, por lo que va en dirección al 0 y, en este caso, la derivativa precide que ya ha corregido suficiente y lo corrige precísamente hacia el lado contrario para que encuentre el setpoint.
- El robot tiene un error de -24 y luego de +25: derivativa = 25 - -24 = 49; El error ha cambiado de signo y ha aumentado 49 (o 25 en el lado positivo): corrección = 25 + 49 = 74. En este caso, puede que el control proporcional no detecte ese cambio brusco, pero la derivativativa si ve la dirección que lleva el robot y fuerza a una rectificación fuerte. Imaginemos el caso de error -24 y luego 0. El control proporcional no rectificaría nada, pero cláramente, el robot está en la dirección de salirse por el lado positivo. El derivativo si detectaría una diferencia de 24 y corregiría el rumbo en consecuencia.
Como se puede ver, sobretodo en el tercer caso, la derivativa calcula la dirección del robot y lo rectifica antes de tiempo, cosa que el control proporcional no puede. Es, por tanto, el factor más importante para la estabilidad del robot.
Hay que tener el cuenta estas consideraciones sobre el control derivativo:
- Cuando el error es constante el derivativo es 0 y no actua.
- Si tenemos mucho ruido en las lecturas, la derivada será muy caótica y provocará movimientos bruscos.
- Si ajustamos bien el Kd, la derivativa ayuda mucho a la integral y proporcional a llegar al Setpoint.
Todos estos métodos pueden modificar mucho la velocidad o demasiado poco. Por ello, se recomienda hacer lo siguiente:
- Probar una velocidad base aceptable.
- Poner todos los K a 0 e ir probando a aumentar el Kp poco a poco hasta que no salga de la línea. Cuanto más lo subamos, más oscilará, por lo que hay que dejarlo justo cuando empieza a oscilar.
- Ir aumentando Ki hasta que empiece a oscilar más y dejarlo por debajo de esos valores.
- Ki, en este robot, modifica demasiado su comportamiento en valores muy bajos. Por tanto, si no se ve claro, mejor dejarlo a 0.
- Ir aumentando Kd hasta que funcione bien.
- Kd es en lo que más vamos a notar su mejora. Además, tiene un rango de valores muy ámplio en el que funciona razonablemente bien.
- Aumentar la velocidad y los demás ajustes hasta que esté a nuestro gusto, (que nunca ocurrirá)
Mejoras
La primera mejora tiene que ver con un problema con la integral. Si pensamos en lo que puede pasar, si el robot está demasiado tiempo fuera de su posición, acumula mucho error. Este, en teoría, es neutralizado con el error de otro signo en el otro lado, pero si es demasiado, puede que no se neutralice y se salga por el otro lado. Esto se llama overshooting.
Sin embargo, esto no tiene porqué ocurrir, ya que, si detectamos que ahora el error acumulado tiene el signo distinto al error actual, es porque hemos pasado de un lado a otro de la línea. Tan solo tenemos que poner la integral a 0:
error = posición - 3500 integral = integral + error si ((posicion*integral)<0) integral=0 // A esto se le llama integral Windup. derivativa = error - error_anterior corrección = Kp * error + Ki * integral + Kd * derivativa velocidad_izquierda = base_izquierda + corrección velocidad_derecha = base_derecha - corrección
La segunda mejora es hacer que corra más cuando está en una recta. El robot puede saber que está en una recta cuando el error es muy pequeño. Si el error es pequeño, la corrección proporcional será mínima, la integral se modificará poco (y teóricamente será cercana a 0) y la diferencial será también mínima. Por lo que el robot tendrá giros muy suaves. Al igual que con un coche real, cuando no tenemos curvas, podemos aprovechar para ir más rápido sin miedo a salirnos. Por ello, podemos establecer una velocidad máxima y por tanto una diferencia entre la velocidad base y la máxima. Esa velocidad será sumada a las dos ruedas por igual antes de las posibles correcciones PID. De esta manera, cuando detecta que puede estar en una recta, el robot correrá más.
error = posición - 3500 integral = integral + error si ((posicion*integral)<0) integral=0 derivativa = error - error_anterior corrección = Kp * error + Ki * integral + Kd * derivativa velocidad_recta = diferencia*exp(-Kv*abs(Kp*error)) // a más error, mucha menos velocidad velocidad_izquierda = base_izquierda + velocidad_recta + corrección velocidad_derecha = base_derecha + velocidad_recta - corrección
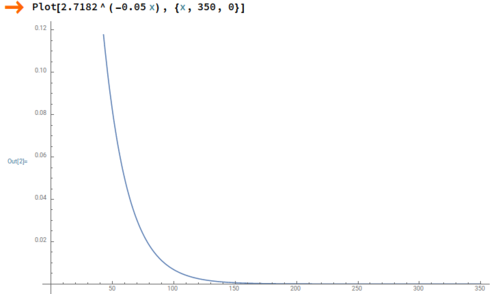
Ahora tenemos dos cosas más a ajusta, la diferencia entre la máxima y base y Kv, que es un factor de corrección. Cuanta más velocidad se pueda sumar a la base, mayor diferencia habrá entre la mínima y máxima. Podemos tener una mínima muy baja para tener más control y una máxima muy alta. Sin embargo, esto puede hacer que se salga cuando llegue a una curva. Tambien podemos ajustar Kv para que afecte más o menos el error. Cuanto más alto sea, más frenará al mínimo error. ¿Y cual es el valor ideal de Kv i de diferencia de velocidad? En cuanto a la diferencia de velocidad, pensemos que, si no hay error, no habrá casi correcciones, por tanto, pensemos en la velocidad máxima (255), la base (100, por ejemplo), pues si le damos 100 de diferencia, como máximo tendremos los dos motores a 200, que es una buena velocidad. Podemos poner más o menos en función de si se sale en las curvas. Por otro lado, el Kv es más complicado. Vamos a utilizar una herramienta disponible para todos, el Wolfram Alpha. En su aplicación web, podemos poner la fórmula Plot[2.7182^(-0.05 x), {x, 350, 0}] para que muestre esta gráfica:
Hemos probado con otros números y 0.05 para 350 de error máximo se ve que hasta casi 50 de error hay una asíntota, por lo que el resultado será 1 o casi 1. A partir de 50 desciende muy rápido, que es lo que queremos.
La tercera mejora consiste en asegurarse de que el comportamiento del robot es instantáneo. Por ejemplo, si un motor tiene 0 de velocidad, que se accione el freno para pararlo más rápido. También nos puede servir para tener un valor máximo (por ejemplo: 250 o 255) y mínimo de velocidad (0) de manera que si el PID calcula una corrección que da una velocidad negativa o superior a 255 el motor no actúe de forma extraña. Por tanto, establecemos una velocidad máxima y mínima y si se alcanza la mínima, activamos el freno.
Y aquí tenemos, por fin, el algoritmo para arduino con PID para 8 sensores a falta de ajustar Kp, Ki, Kd, Kv i la diferencia:
error = (position - 3500); // Para el control proporcional
error = error / 10;
if (((long)error*(long)integral)<0)
{ integral=0; } // A esto se le llama integral Windup.
integral = integral + error; // La integral
derivativa = error - error_anterior; // La derivativa
correccion = Kp * error + Ki * integral + Kd * derivativa;
velocidad_recta = diferencia*exp(-Kv*abs(Kp*error)); // a más error, mucha menos velocidad
if(Kv == 0) velocidad_recta=0;
leftMotorSpeed = base_iz + velocidad_recta + correccion;
rightMotorSpeed = base_der + velocidad_recta - correccion;
error_anterior = error; // Para la derivada
/////// La parte de frenar y limitar las velocidades
if(leftMotorSpeed > vel_maxima) { leftMotorSpeed = vel_maxima; digitalWrite(A3, HIGH);}
if(rightMotorSpeed > vel_maxima) { rightMotorSpeed = vel_maxima; digitalWrite(A3, HIGH);}
digitalWrite(8,LOW); // Quitamos el freno antes de decidir si lo ponemos
if(leftMotorSpeed <= vel_minima) { leftMotorSpeed = vel_minima; digitalWrite(8,HIGH); /*digitalWrite(A3, HIGH);*/} // El freno
digitalWrite(9,LOW); // Quitamos el freno antes de decidir si lo ponemos
if(rightMotorSpeed <= vel_minima) { rightMotorSpeed = vel_minima; digitalWrite(9,HIGH); /*digitalWrite(A3, HIGH);*/} // El freno
analogWrite(3, rightMotorSpeed); //Spins the motor on Channel A
analogWrite(11, leftMotorSpeed); //Spins the motor on Channel B
Y el programa entero del robot
https://en.wikipedia.org/wiki/PID_controller
Control por Bluetooth
Sin modificar el programa, se puede añadir un receptor bluetooth HC-06, por ejemplo y recibir los datos de telemetría en el móvil o PC.
Antes de hacerlo, recomiendo leer el otro tutorial del Robot teledirigido por bluetooth
Podemos poner los cables como en este esquema:
Y, como ya tenemos la impresión por el puerto serie, no hace falta modificar el código.
Una vez tenemos el Bluetooth, podemos hacer un programa en Android o para Ubuntu que muestre gráficas o permita modificar los parámetros Kp, Ki, Kd en el momento.
En nuestro caso, hemos instalado la aplicación Bluetooth Serial Controller y configurado para tener esta apariencia y enviar letras como s,w,P,p,I,i,D,d,V,v,B,b. Con estas letras, modificaremos los parámetros del PID y la velocidad Base, además de permitir arrancar o parar el coche con el teléfono móvil. Estas modificaciones agilizan muchísimo el ajuste del PID a los valores ideales, ya que se ve el comportamiento de cada modificación en tiempo real.
Luego en el programa del robot, hacemos que con los botones se controlen los diferentes parámetros en tiempo real.
Observemos la función controlador(), donde modificamos los parámetros del programa en función de lo que pide la App por Bluetooth:
void controlador(){
char option = Serial.read();
if (option == 'w') { inicio=true; Serial.println("Start");}
if (option == 's') { inicio=false; Serial.println("Stop"); analogWrite(3, 0); analogWrite(11, 0); }
if (option == 'P'){ Kp+=0.01; }
if (option == 'p'){Kp-=0.01; }
if (option == 'I'){ Ki+=0.001; }
if (option == 'i'){Ki-=0.001; }
if (option == 'D'){ Kd+=0.1;}
if (option == 'd'){Kd-=0.1; }
if (option == 'V'){ Kv+=0.001;}
if (option == 'v'){Kv-=0.001;}
if (option == 'B'){ base_iz+=1;base_der+=1;}
if (option == 'b'){base_iz-=1;base_der-=1;}
Serial.print(Kp); Serial.print(' '); Serial.print(Ki); Serial.print(' ');
Serial.print(Kd); Serial.print(' '); Serial.println(Kv); Serial.print(' ');
Serial.println(base_iz);
}
Y aquí todo el programa:
Si, además, queremos telemetría, podemos descomentar los prints.
Telemetría
Descomentando los prints del programa y con los valores Kp=0.5, Ki=0.01, Kd=1 y Kv=0.05, hemos conectado el robot por Bluetooth al PC y guardado los datos que nos envía. Una sección de estos datos es como esto:
920 | -258 -1810 -4 -153 0 971 | -252 -2062 6 -143 0 1648 | -185 -2247 67 -49 0 2012 | -148 -2395 37 -62 2 2803 | -69 -2464 79 19 17 3221 | -27 -2491 42 3 50 3725 | 22 22 49 60 57 3867 | 36 58 14 32 39 3884 | 38 96 2 22 37 3781 | 28 124 -10 5 48 3713 | 21 145 -7 5 58
Donde la primera columna es la posición, error, integral, derivada, corrección y velocidad en recta.
Estos datos los formateamos con este comando:
cat -n telemetria | tr '\t' ' ' | tr -s ' ' | tr -d '|' > datostelemetria
Y luego podemos dibujar una gráfica con Gnuplot:
set style data lines plot 'datostelemetria' using 1:3 title 'error', \ 'datostelemetria'using 1:4 title 'integral', \ 'datostelemetria'using 1:5 title 'derivada', \ 'datostelemetria' using 1:6 title 'correcion', \ 'datostelemetria' using 1:7 title 'vel. recta'
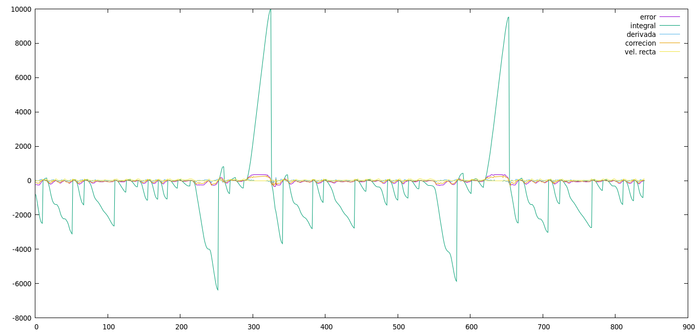
El resultado en este caso es esta gráfica:
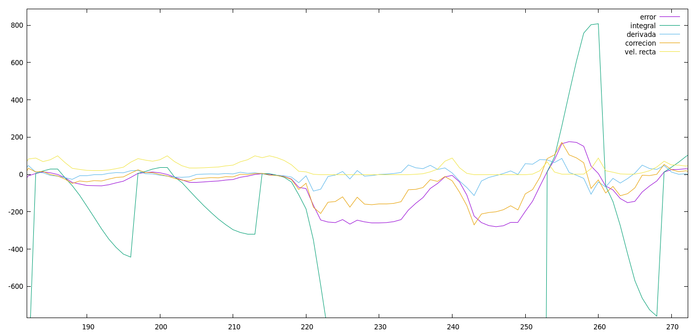
Aquí no se puede ver gran cosa, tan solo los grandes incrementos de la integral cuando se sale de las curvas. Si acercamos un poco el zoom sobre alguna zona, tenemos ya algo interpretable:
En este gráfico se puede ver cómo aumenta la integral mientras el error siga del mismo signo y cómo se pone a 0 cuando cambia de signo. Esta integral está haciendo oscilar un poco al robot, ya que incrementa la corrección aunque ya esté en la dirección correcta. Esto se compensa un poco con la derivada. Otra cosa que está haciendo la integral es centrar el error. En este caso, nuestro robot tiene un motor un poco menos potente que el otro y parece que tiende a tener más error negativo que positivo. La integral compensa esto aumentando la velocidad de este motor. Hay que pensar qué interesa, si centrar el error respecto al 0 o no tenen oscilaciones.
En cuanto a la derivada, se ve cómo cambia mucho con pequeñas variaciones del error. Incluso en momentos donde el error sigue aumentando, pero a menos ritmo, se ven cambios bruscos en la derivada, ya que ha detectado un cambio de dirección y, por tanto, su influencia debe ser menor.
La velocidad en recta es 0 cuando hay un error grande y llega a casi 100 en los momento más estables.
A partir de estos datos, podemos concluir que hay una tendéncia a tener más error negativo que positivo, lo cual se puede achacar a los motores o al diseño del circuito, con la integral esto se corregiría, a riesgo de tener más oscilaciones. También que todos los factores están influyendo correctamente (esto no es trivial, ya que pueden haber errores en las instrucciones matemáticas como cambios de signo que, por su poca influencia no se perciban a la vista pero empeoren el movimiento del robot). Por último, en cuando a la velocidad en recta, se demuestra que un valor de 0.05 en nuestro caso es bastante adecuado, ya que incrementa la velocidad hasta casi la máxima y la decrementa exponencialmente al mínimo error.
Enlaces
- (Obsoleto) Manual de la biblioteca del sensor Referencia de la biblioteca
- (Versión 4.) Manual Referencia
- Tutorial en castellano
PID:
- Tutorial en Castellano
- Otro Tutorial en castellano con ejemplo de código
- Muy buen tutorial en castellano y con simulador Ajustar un controlador PID Implementar un PID en arduino
Ver también: